
Puzzles, conundrums and lateral thinking exercises help team building, motivation, and will warm up any gathering. Puzzles and conundrums like these are great brain exercises, and are good illustrations of how the mind plays tricks. See also the puzzles and tricks page, the team building games section for team building and employee motivation ideas, and try the expressions derivations quiz on the cliches origins section. Puzzles and lateral thinking exercises add interest to meetings and training sessions. Giving groups or teams a mixed set of puzzles is a great way to get people working together and using each other's strengths.
These lateral thinking exercises and complex puzzles are great for making people think, opening minds to new possibilities, and illustrating how the mind plays tricks and the importance of using the brain, instead of making assumptions.
This is a fabulous demonstration of the power of faith in random decision-making over simple logic and probability. It was inspired by the format of an old USA TV gameshow 'Let's Make A Deal', hosted by Monty Hall, and the conundrum is commonly referenced in various forms by scientists and writers when demonstrating widely ranging aspects of probability theory and how the mind works.
Broadly the game show conundrum was:
A contestant is shown three closed doors. Behind one door is $10,000; behind the other two is nothing (or in some versions of the story, a goat). The contestant is invited to choose one of the doors and keep whatever lies behind. This offers a one-in-three-chance, ie., 1/3 or 2:1, of winning. That is to say the contestant had a one in three chance of picking the right door.
When the contestant had chosen a door, Monty Hall then opened one of the other doors to reveal nothing behind it (or a goat), which left two closed doors, one with the money behind it and one with nothing (or a goat). The contestant was then asked if they wish to change their original choice, which creates the conundrum:
Have the odds changed as to which door wins and which door loses? And if so how?
What would you do? Keep your original choice, or choose the other door?
Most contestants on Monty Hall's show were reluctant to change their original choice for fear that it was right, or because intuitively they felt that probability could not be altered by revealing one of the 'losing' doors. The problem is called 'counter-intuitive', because the answer seems for many to defy instinct and logic, even after it's been explained several times.
You should change your choice, and here are a couple of ways of justifying why (mathematicians and probability experts can provide plenty more complex explantion than this if you need it):
The door you originally chose was a one-in-three chance - ie, the likelihood of your guessing that door to be the winning door was one-in-three. The 'other' door is now a one-in-two chance, and the likelihood of your guessing the 'other' door to be the winning door is one-in-two. You are 50% more likely to correctly guess a one-in-two chance than a one-in-three chance, so pick the other door in preference to your original choice of door.
The door you originally chose was a one-in-three chance. The other two doors collectively represented a two-in-three chance. When one of these doors is eliminated, the two-in-three odds transfer to the other remaining door, which you should now chose in preference to your original door, which was a one-in-three chance.
Logic and the law of probability says to switch original choice and pick a different door.
If you're still in doubt, imagine there are 20 doors - one has the money, the others nothing. You pick a door, then 18 doors are opened revealing nothing, leaving your choice and the one other door. Would you change your choice now? By switching doors you'd improve your chances from one-in-twenty, to '50:50' evens, or (depending on how you look at it) arguably nineteeen-in-twenty. Do you change your choice? It's staggering how many people still refuse to.
Still sceptical? How about 100 doors: Pick a door. Open 98 revealing nothing, leaving two doors, one a winner and the other a loser. Would you still prefer your original 99-to-1 shot compared to the alternative which is at worst 50:50, and arguably a massive 99% chance?
More technical explanation at http://www.io.com/~kmellis/monty.html
(Thanks to Rupert Stubbs and Wendy Ramsay for suggestions and guidance.)
This amazing model was based on a traditional gambling game, and brought to prominence particularly by the American political scientist Robert Axelrod. The prisoner's dilemma has been studied and discussed for decades by strategists, gamblers, philosophers, and evolutionary theorists (see note about Richard Dawkins below).
Here's how the gambling game works (at a simple level it's great for demonstrating the dangers of selfish behaviour, and the benefits of co-operation):
There are two players or teams. Each has two cards, one marked 'Defect', the other 'Co-operate'. There is a neutral banker, who pays out or collects payments depending on the two cards played. Each player or team decides on a single card to play and gives it to the banker. The banker then reveals both cards.
Here's the scoring system:
Try it. The tendency if for each team to play Defect all the time, in hope of the big payout, and as a defence against being 'suckered' and having to pay the big fine. But where do these collective tactics lead? In the end the banker will collect all the money, albeit at £10 per round, but the banker always wins and both players always lose.
After a while, the players realise that their only hope for survival and beating the banker is to co-operate. Of course along the way, one or other players might be tempted to play 'Defect' and will collect the big payout having exploited the trust of the other side, but is this a sustainable strategy? Of course not. It reignites the tit-for-tat aggressive defence scenario when both sides play 'Defect' and both sides lose.
Try playing the game with a group of people who randomly pair up for each round (single show of cards). Again, some players will attempt a strategy of continuous 'Defect'. Their gains however will be short-lived. Pretty soon they'll get a reputation for being selfish and no-one will play them, let alone co-operate.
Professor Richard Dawkins, Fellow of New College, Oxford, provides more fascinating explanation about this model and just how fundamental it is to our existence in his book ' 'The Selfish Gene'.
The model is called the prisoner's dilemma after the traditional story of two prisoners who are suspected of a crime and captured. The evidence is only sufficient to achieve a short custodial conviction of the pair, so they are separated for questioning, and each invited to betray his partner in exchange for their freedom. Not permitted to meet and discuss their decision, they each face the following prisoner's dilemma:
A man travel by car to a destination 25 miles away. The journey was made between 7 and 9am, so the roads were congested and progress was slow. The journey took 75 minutes, which means that his average speed was 20 miles per hour. He took the same route on the return and travelling in the middle of the day made faster time: his return journey lasted just 25 minutes, meaning that his average speed fro the return journey was 60 miles per hour.
What was his average speed for the two journeys combined?
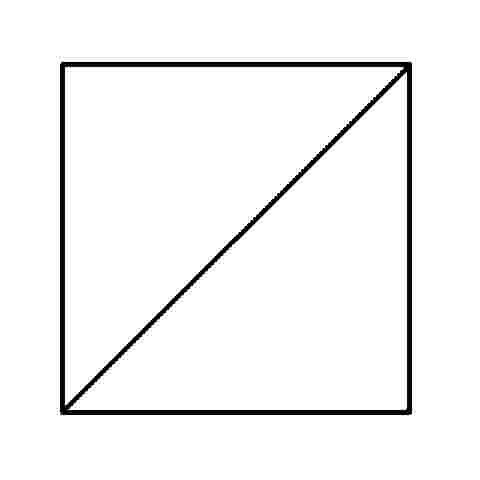
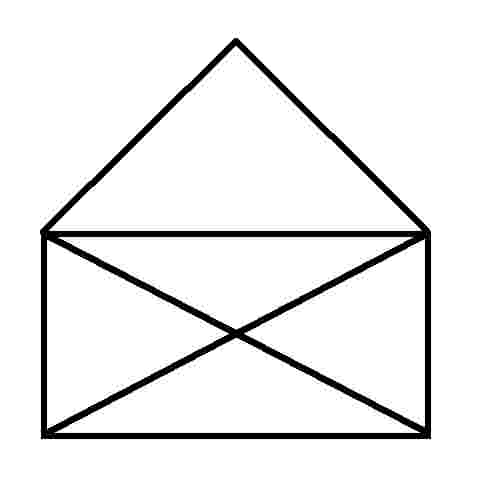
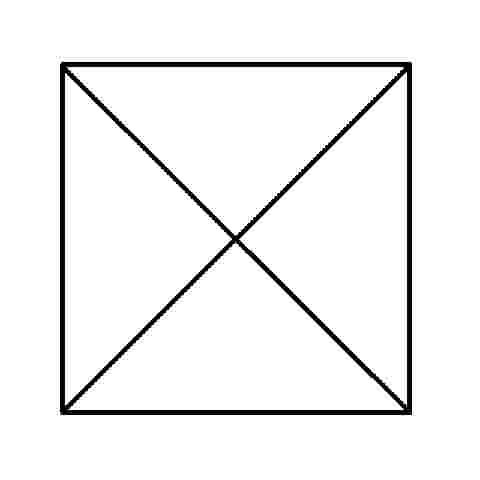
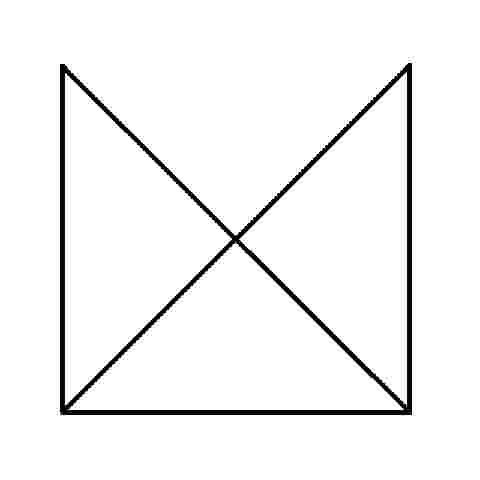
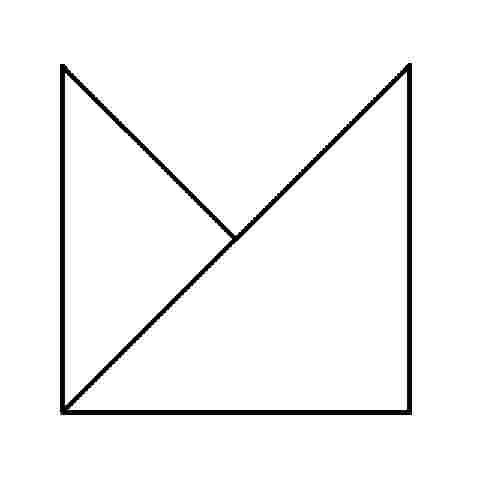
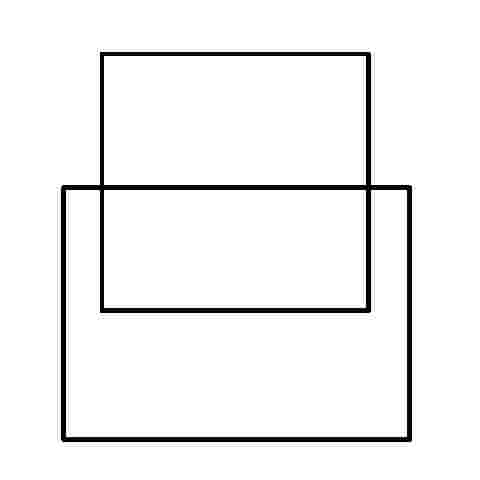
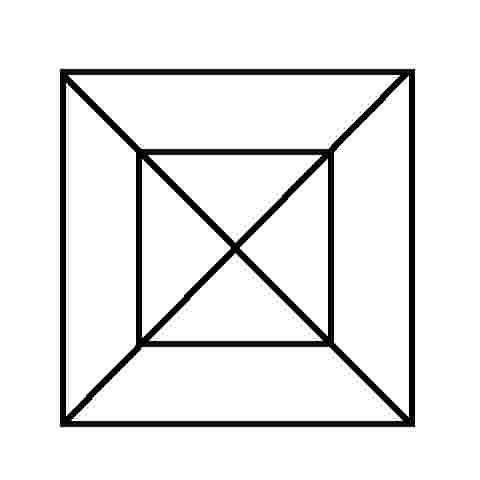
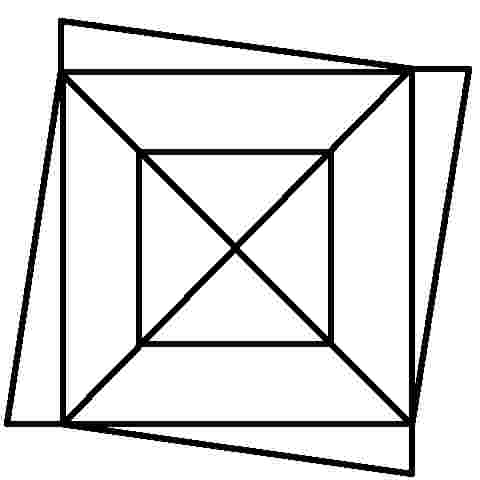
We've all seen these geometric puzzles which challenge you to trace along all of the lines, without lifting the pen from the paper and tracing each line only once. How many of these puzzles can you complete? How many of these puzzles are possible and how many are impossible? Is there a way of knowing whether a puzzle of this sort is possible without trying it? There is. Try them first and then check the answers, as well as learn the secret.
When you know the Euler's Rule it's easy to make up your own puzzles like these, and be confident of whether they are possible or not - all you need is a pen and a flip-chart: great for coffee break diversions, team building exercises, etc.
| Puzzle 1 - Easy ones first?...... |  |
| Puzzle 2 - Still easy? Can it be done?.... |  |
| Puzzle 3 - Looks easy, but not so easy. Can it be done? |  |
| Puzzle 4 - Now this one is easy... |  |
| Puzzle 5 - Easy. |  |
| Puzzle 6 - Easy. |  |
| Puzzle 7 - Looks very difficult. Can it be done? |  |
| Puzzle 8 - Don't even try this one... |  |
| Puzzle 9 - It's got something to do with where you start... |  |
| Puzzle 10 - Same applies here - where you start makes all the difference - assuming it can be done... |  |
| Puzzle 11 - Like I said, assuming it can be done... |  |
| Puzzle 12 - It would be a pity to end with one that's impossible... |  |
I call them euler puzzles after the man who devised the method of knowing if they are possible or not. Leonhard Euler was a brilliant 18th century mathematician who solved the puzzle of the Konigsberg bridges (now Kaliningrad, in Russia). Seven bridges connected both sides of the city and two islands in between. The townsfolk passed their time for many years trying (unsucessfully) to find a route which would cross each bridge only once. Euler proved that is was not possible, until an eighth bridge was constructed (unfortunately litte remains of the original city or its bridges since the 2nd world war). Nevertheless Euler's Rule survives, and is now used in planning routes and service territories (for postal services, meter reading, door-to-door deliveries, etc) the world over, to eliminate unnecessary travel and back-tracking. So what's the secret?
For all the answers and Euler's Rule go here.
More complex puzzles and conundrums will added from time to time, so please keep visiting this page. If you have a puzzle or conundrum of your own that you'd like featured on this page (with suitable acknowledgement of course) please send it.
More quicker puzzles and tricks are on the main puzzles page.
See also the great ditloids puzzles, the cliches and words origins quiz, and the team building games section.
The use and reproduction of this material is free for research or organisational development purposes, provided copyright (Alan Chapman 2001/2/3) is acknowledged and reference or link is made to the www.businessballs.com website. This material may not however be sold, reproduced for general publication in any form, or used in the provision of business services to a third party, without prior agreement and permission from Alan Chapman. Disclaimer: Reliance upon any information or material on this website, or advice received from Alan Chapman, shall be at your sole risk. Alan Chapman assumes no responsibility for any errors or omissions or for the results obtained from the use of such information, and is not liable for any damages of any kind resulting from the use of, or reliance on, the information and material contained on this website, advice given directly by Alan Chapman in response to enquiries, or any third party website linked to this website. Readers and users of this website are encouraged to confirm the information contained herein with other sources, and most definitely to seek local relevantly qualified advice if embarking on any actions that may potentially carry liabilities, of personal, organisational or any other type. Managing people and relationships are sensitive activities; the free material and advice available via this website do not provide all necessary safeguards and checks for organisations or individuals.
© alan chapman 2001/2/3
| The river banks and islands are nodes. The bridges are effectively lines connecting these nodes. Prior to the construction of the eighth bridge (shown on the left in dotted lines, the puzzle was impossible because there were four odd nodes (count the number of bridges from each of the two river banks - 3 - and two islands - 5 and 3). When the eighth bridge was built the river bank nodes became even nodes with four bridge connections each, leaving only two odd nodes, and a solvable puzzle. | 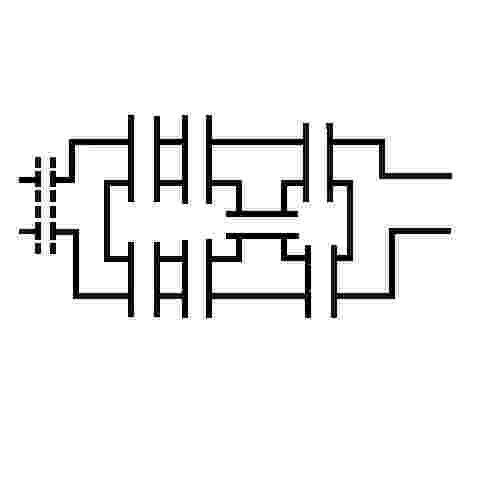 |
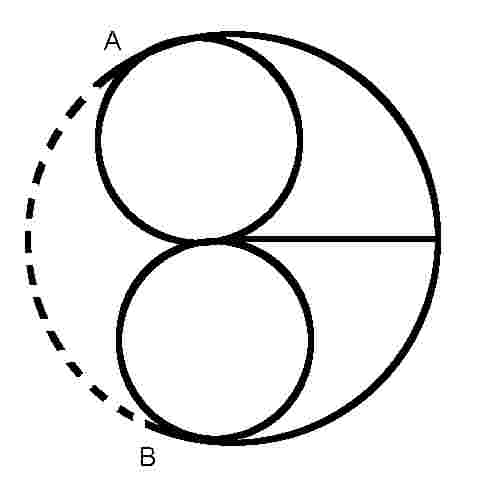
| Here's a network diagram of the same thing
- a topological map; the topology method of simplyifying network analysis
was also invented by Euler. The nodes at A and B have been changed from
odd to even with the dotted line, which is the eighth
bridge. (Incidentally, the famous London Underground Map is another example of a topological map - it's not geographically accurate at all, but it is very much easier to understand than a pure geographical map.) If you want to read more about this and other fascinating mathematical puzzles and explanations read 'Why Do Buses Come In Threes?' and the follow-up 'How Long Is A Piece Of String?' by Rob Eastaway and Jeremy Wyndham. |
 |
The use and reproduction of this material is free for research or organisational development purposes, provided copyright (Alan Chapman 2001/2/3) is acknowledged and reference or link is made to the www.businessballs.com website. This material may not however be sold, reproduced for general publication in any form, or used in the provision of business services to a third party, without prior agreement and permission from Alan Chapman. Disclaimer: Reliance upon any information or material on this website, or advice received from Alan Chapman, shall be at your sole risk. Alan Chapman assumes no responsibility for any errors or omissions or for the results obtained from the use of such information, and is not liable for any damages of any kind resulting from the use of, or reliance on, the information and material contained on this website, advice given directly by Alan Chapman in response to enquiries, or any third party website linked to this website. Readers and users of this website are encouraged to confirm the information contained herein with other sources, and most definitely to seek local relevantly qualified advice if embarking on any actions that may potentially carry liabilities, of personal, organisational or any other type. Managing people and relationships are sensitive activities; the free material and advice available via this website do not provide all necessary safeguards and checks for organisations or individuals.
© alan chapman 2001/2/3